There are many stereotypes on what the power and torque of a car or motorbike actually represent. Some are, "power shows how fast a car is and torque how powerful". "for low speed power you need a lot of torque in low rpm", "a diesel car is more powerful than a high-revving petrol engine one" etc

All of the examples above are either over-simplifications or plain wrong. However someone with not much knowledge on the subject may use them to fractionally describe the feeling a car gives him, which is why these stereotypes are so dominant.

That is why we will start from the very basic:


energy, power

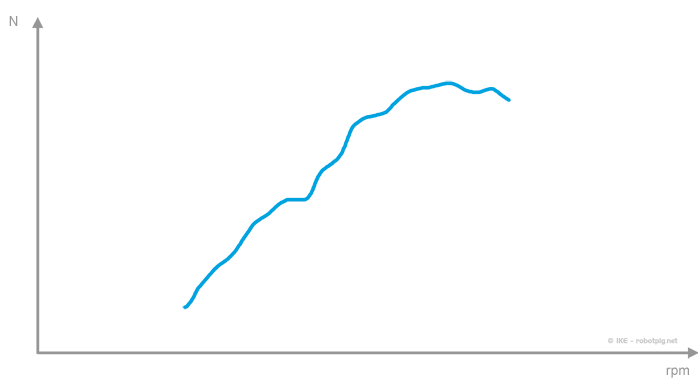
What we mostly demand from a car (or motorbike) is for it to be able to transport its payload (passengers etc) and also to be able to accelerate and/or withhold its velocity while ascending or generally in a variety of circumstances. That is of course the reason the engine exists. It produces power that eventually will reach the tires and propel the vehicle. In internal combustion reciprocating engines the power delivery is a function of many parameters. If we assume that we examine an engine in full throttle and by eliminating other exogenous factors (fuel quality, temperature, wind resistance etc) we can propose with good approximation to our subject, that an engine delivers power as a function of its rotating speed (in rpm).
Thus we can take as a given that an engine delivers the same power when rotating at a specific rpm. (ex at 3500rpm it produces 100ps).

If we take a look at any power diagram like the one below, it is obvious that every engine has a specific operation span and if we want to exploit in the best way possible the power that the wheels receive (ex to accelerate or to climb a steep road) we have to introduce a mechanism in order for the engine to operate in the rotating speed span where it performs the best.

The engine is connected to the wheels via the transmission thus the engine rotating speed is always proportional to the vehicle velocity. The integral transmission system (gearbox, differential and wheels) is the mechanism we mentioned above that 'synchronizes' the engine rotation speed with the velocity of the vehicle and makes possible for the engine to operate in a relatively optimum rpm range in respect to the vehicle velocity.

Until now we have already mentioned power several times but not once the term torque. As we will better examine below, torque is a quantity that constantly changes during the transition from one system to another. Power is the only quantity that remains unchanged (with the exception of losses of course).



power flow

What is the relation between torque and power? In a non-rotating system, if for example we have a mass that moves in a straight line, the power according to Newton mechanics is the energy rate of change. We can express power as a function of velocity and the formula is: power equals velocity times the force.

Thus the power we need in order to move slowly a heavy object is the same with the power needed to move a light object fast. In our case where the system is rotating, power is equal to the product of angular velocity (rpm) times the torque. We can have the same power consumption when a big torque rotates slowly or when a small torque rotates fast.

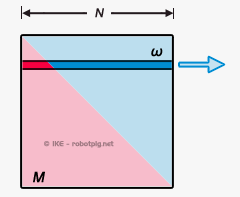
To better comprehend the relation between power, angular velocity and torque we will use the diagram below with the 'power square' (more on this on the special box on the right).

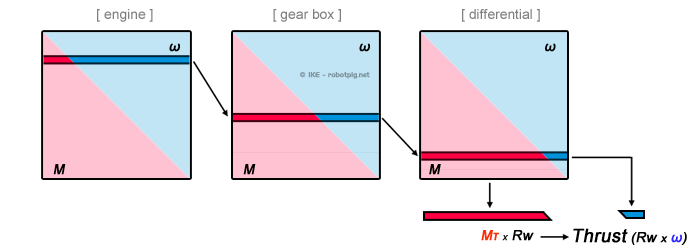(M=torque, ω=angular velocity, Rw=wheel radius)

In the image above we can see that the -constant- amount of power that for a given rpm an engine produces is represented by the width of the square. In every stage of the transmission system we can select the 'level' we want inside the square in order to have the combination of rpm and torque we want. This combination at the final stage (differential) will relate the rpm with the vehicle velocity and the product of this torque and the wheel radius gives us the force the tire excels on the road (thrust).

It is worth mentioning here that the transmission system is maybe equally important to the engine. As it can be seen in the diagram below, we can reach to exactly the same thrust in the wheel (for given velocity) from two different engines (K1 and K2) with completely different power delivery characteristics by using different gear ratios:


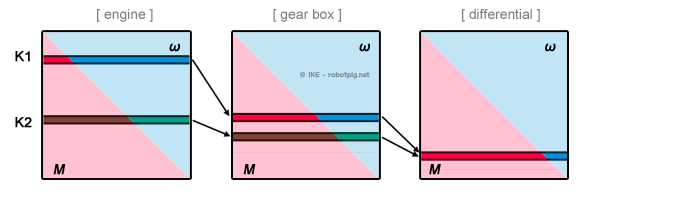
If we had only one fixed gear ratio (where a certain rpm of the engine reflects a specific velocity for the vehicle) then we could exploit the power delivery of the engine only in a very narrow span of vehicle velocity.

This is the reason the gearbox exists. By using it we can control the relation between vehicle velocity and engine angular velocity and use the optimum engine operation range in a bigger vehicle velocity span:


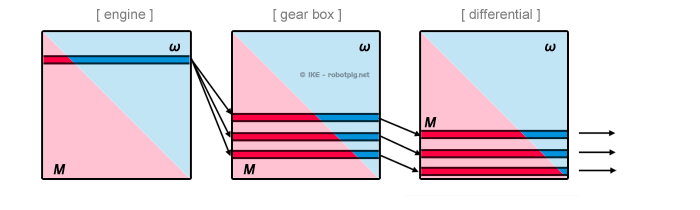
It is obvious that with a 3-speed gearbox we can operate the engine at its very peak point of power delivery for three distinct velocities. In the between the engine yields less power and this can be reproduced in the diagram above if we can assume a narrower square that represents the non-optimum power delivery for the velocities between these 3.