καμπύλες ώσης

Για να δούμε λοιπόν στην πράξη πόση δύναμη φτάνει στο σημείο επαφής του ελαστικού με το δρόμο χρειαζόμαστε το διάγραμμα ώσης, για να το κατασκευάσουμε χρειαζόμαστε τα εξής:

- καμπύλη ισχύος
- λόγους μείωσης ταχυτήτων
- λόγο μείωσης ενδιάμεσου κιβωτίου*
- λόγο μείωσης διαφορικών
- διάμετρος τροχού

*transfer case, οι "αργες-γρήγορες" σχέσεις που έχουν πολλά τετρακίνητα μοντέλα

Με τα παραπάνω στοιχεία και με τη βοήθεια του τύπου που ακολουθεί προκύπτει το διάγραμμα ώσης,

ώση=(ισχύς/στροφές ανά λεπτό)*(λόγος μείωσης 1ης ταχύτητας)*(λόγος μείωσης transfer)*(λόγος μείωσης διαφορικού)*(2/διάμετρος τροχού) (ομοίως για 2α,3η κλπ)

Οι καμπύλες που προκύπτουν για κάθε ταχύτητα είναι:


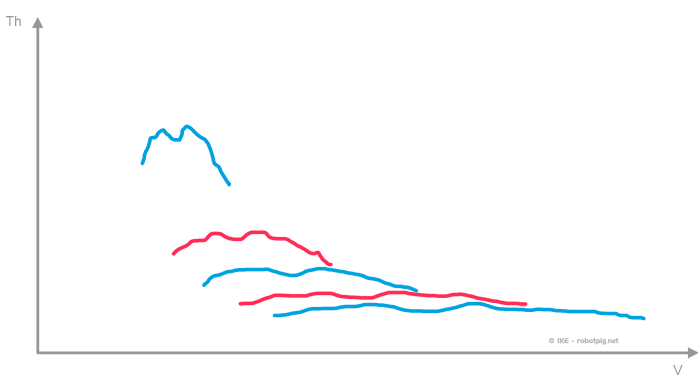
και το ενιαίο σχήμα για όλες τις σχέσεις αντίστοιχα:




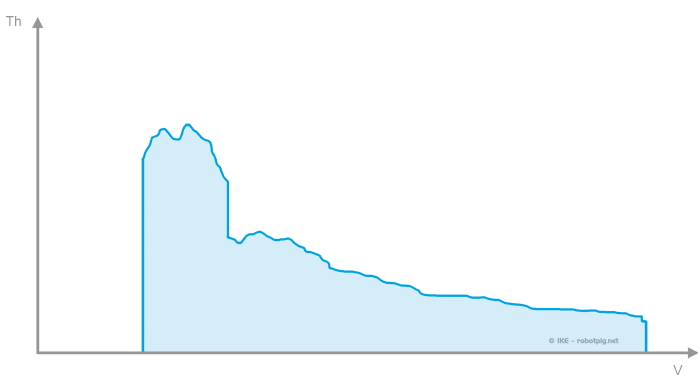
Το παραπάνω διάγραμμα έχει στον οριζόντιο άξονα την ταχύτητα κίνησης και στον κατακόρυφο την διαθέσιμη ώση (δύναμη) στους κινητήριους τροχούς.

Όπως είναι προφανές το διάγραμμα καμπύλων ώσης δεν είναι παρά το διάγραμμα της ισχύος ανηγμένο για κάθε σχέση του συστήματος μετάδοσης. Εδώ μπορούμε να εντοπίσουμε μια από τις συνηθέστερες παρεξηγήσεις:

Το να κρίνουμε πόσο δυνατό είναι ένα αυτοκίνητο με βάση την τιμή της μέγιστης ιπποδύναμης (ή ροπής) είναι σαν να πετάμε την καμπύλη από το διάγραμμα και να κρατάμε μόνο 5 (αν έχουμε 5τάχυτο κιβώτιο) σημεία. Και μάλιστα αν δεν συνυπολογίσουμε τα μεγέθη του συστήματος μετάδοσης δεν μπορούμε να έχουμε ούτε τα σημεία αυτά καθώς δεν θα γνωρίζουμε την θέση τους ούτε στον οριζόντιο ούτε στον κατακόρυφο άξονα. Αυτό που απομένει είναι ένα σημείο (αυτό της μέγιστης ισχύος) που στην πραγματικότητα από μόνο του δεν σημαίνει τίποτα.



διαδρομή αναφοράς

Για να γίνουν τα παραπάνω πιο κατανοητά θα τα εφαρμόσουμε σε ένα παράδειγμα με αρκετές εφαρμογές ώστε να καλύψουμε τις περισσότερες περιπτώσεις. Για να δούμε λοιπόν πως μεταφράζεται το διάγραμμα ώσης στην πράξη θα το προβάλουμε σε μια διαδρομή αναφοράς.

Θεωρούμε την διαδρομή μιας μικρής πίστας, σχετικά κλειστής (για περισσότερα στο κουτάκι δίπλα) στην οποία ένας τυπικός γύρος μας δίνει το παρακάτω γράφημα με την ταχύτητα κίνησης του οχήματος σε κάθε σημείο:

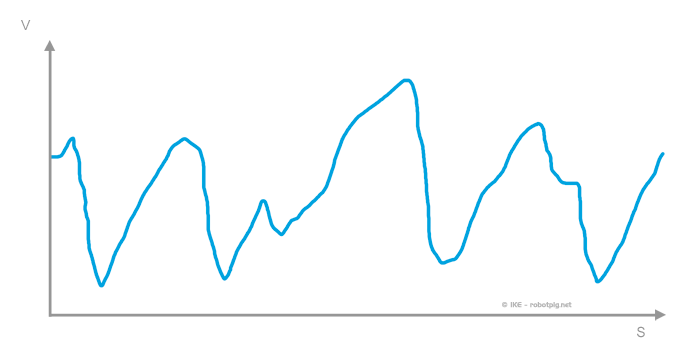
Αν αντιστοιχίσουμε την ώση για την ταχύτητα σε κάθε σημείο της πίστας (από το διάγραμμα ώσης πιο πάνω) θα έχουμε το διάγραμμα ώσης / απόστασης για τη συγκεκριμένη πίστα (και τις συγκεκριμένες ταχύτητες κίνησης!).
Έτσι μπορούμε να δούμε σε κάθε σημείο την 'περίσσεια ώσης' που έχει το όχημά μας. Όσο περισσότερη τόσο μεγαλύτερη η ικανότητα του αυτοκινήτου να επιταχύνει ή να έλκει φορτίο.

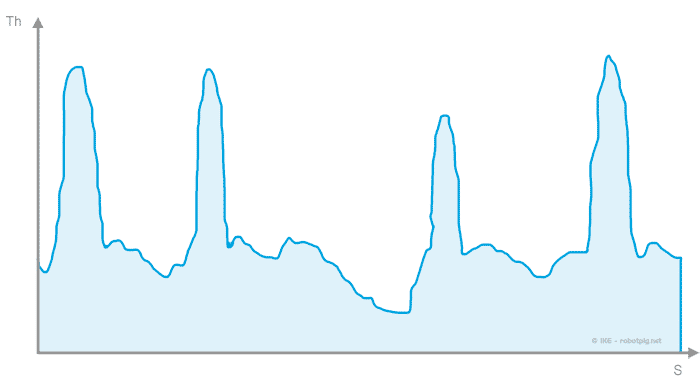
Θα μπορούσε κάποιος να πει πως ένα δυνατότερο αυτοκίνητο θα είχε διαφορετική ταχύτητα ανά σημείο σε σχέση με ένα ασθενέστερο όμως επειδή εδώ μας ενδιαφέρει η σύγκριση θα θεωρήσουμε πως όλα τα αυτοκίνητα που θα διατρέξουν την διαδρομή θα κινηθούν με την ταχύτητα αυτή και θα συγκρίνουμε το πλεόνασμα ώσης στο διάστημα της διαδρομής.(για περισσότερα βλ. παρατηρήσεις).

Επίσης για να εξετάσουμε το θέμα πιο ρεαλιστικά χωρίς να εισερχόμαστε σε οριακές καταστάσεις όπου τα αυτοκίνητα των παραδειγμάτων πιθανώς να μην μπορούσαν να αντεπεξέλθουν αλλά και για να έχουμε μια εικόνα πιο κοντά στη ρεαλιστική οδήγηση τα διαγράμματα για τα αυτοκίνητα υπολογίζονται στο 70% της ταχύτητας αναφοράς (εκτός αν αναφέρεται διαφορετικά), αρκετά πιο κάτω δηλαδή από τον καλύτερο χρόνο πίστας (βλέπε κουτάκι δεξιά) που πάρθηκε σαν μέγεθος αναφοράς.